Another way of writing lens prescriptions is cross-cylinder form. Usually, this form is never used to write spectacle lens prescriptions. However, it gives you an in-depth understanding of the power of each meridian without the need to add or subtract. Or it divides Sphero-cylinder prescription into two Plano cylinders with their axis 90 degrees apart from one another. This cross-cylinder form of prescription writing is one of the methods of calculating gross and net retinoscopy values. It is also a way to represent keratometer readings.
Steps of Sphero cylinder to Cross cylinder
Step 1: To find the first cross-cylinder power, write the spherical power of the sphero-cylinder prescription as it is, but the axis will be 90 apart from the axis of the cylinder in sphero-cylinder form.
Step 2: To find the second cross-cylinder power, add the spherical and cylindrical power of the sphero-cylinder form and the axis will be the same as the axis of the cylinder in sphero-cylinder form.
Example 1:
+5.00 DS / -2.00 DC X 90
Step 1:
1st cylinder = Power similar to sphere power of sphero-cylinder form X axis 90 apart from the axis of the cylinder in sphero-cylinder
1st cylinder = +5.00 DC X 180
Step 2:
2nd cylinder = Algebraic sum of sphere and cylinder power of sphero-cylinder form X axis same as the axis of the cylinder in sphero-cylinder form.
2nd cylinder = +3.00 DC X 90
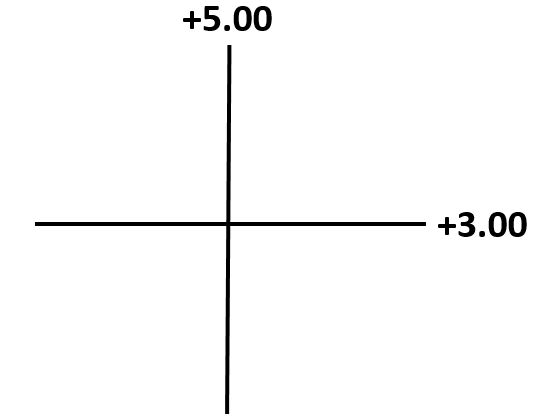
Final = +5.00DC X 180 / +3.00 DC X 90
Alternate cross-cylinder form
Another way of writing cross-cylinder power is instead of mentioning the axis of the cylindrical meridian will mention the power meridian. Remember to use @ which means the power of that particular meridian. Don’t use, X which means axis meridian.
Steps of Sphero cylinder to Alternate cross-cylinder form
Step 1: To find the first cross-cylinder power, write the spherical power of the sphero-cylinder prescription as it is, power meridian will be the same as the axis of the cylinder in sphero-cylinder form.
Step 2: To find the second cross-cylinder power, add spherical and cylindrical power of sphero-cylinder form, but the power meridian will be 90 apart from the axis of the cylinder in sphero-cylinder form.
Example 2:
+5.00 DS / -2.00 X 90
Step 1:
1st cylinder = Power similar to sphere power of sphero-cylinder form, @ power meridian same as the axis of the cylinder in sphero-cylinder form.
1st cylinder = +5.00 DC @ 90
Step 2:
2nd cylinder = Algebraic sum of sphere and cylinder power of sphero-cylinder form, @ power meridian 90 apart from the axis of the cylinder in sphero-cylinder.
2nd cylinder = +3.00 DC @ 180
Final = +5.00DC @ 90 / +3.00 DC @ 180
Power cross
Cross-cylinder form is easier when the cylinder components are visualized on a power cross. It is similar to alternate cross cylinder form but instead of writing in cross form, it will be drawn as a power cross.
For more information watch our YouTube video
Lecturer (Nethradhama School of Optometry)
Moptom


very good