Steps of the cross-cylinder to Spherocylinder
Step 1: Choose either one cross cylinder out of two, as the sphere.
Step 2: Subtract the cross-cylinder which was taken as the sphere from the other cylinder which was not taken as the sphere in step 1.
Step 3: Axis of the sphero cylinder form is the same as the axis of the cross-cylinder which was not taken as the sphere.
Example 1:
-2.00 DC X 180 / +3.00 DC X 90
Step 1:
New Sphere = -2.00DS
Step 2:
New cylinder power = (Cylinder power which was not taken as the sphere in step 1) – (Cylinder power which was taken as the sphere in step 1)
New cylinder power = +3.00 – (-2.00)
New cylinder power = +5.00 DC
Step 3:
90 degrees (Same as the axis of the cross-cylinder which was not taken as a sphere)
Final Sphero cylinder power = -2.00 DS / +5.00 DC X 90
Steps of power cross cylinder to sphero-cylinder
Step 1: Choose either one power meridian out of two, as the sphere.
Step 2: Subtract the power meridian which was taken as the sphere from the other power meridian which was not taken as the sphere in step 1.
Step 3: Axis of the sphero cylinder form is the same as meridian 1 which was taken as the sphere in step 1.
Example 2:
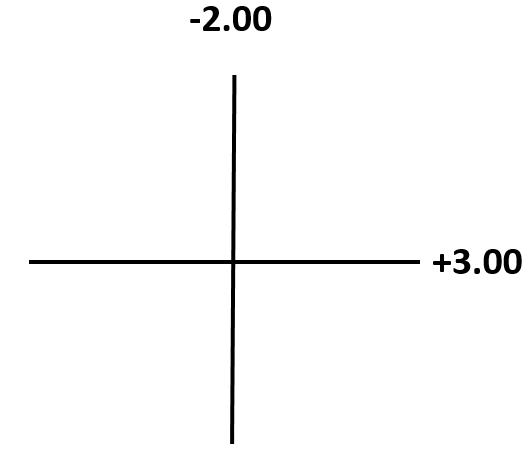
Step 1:
New Sphere = -2.00 DS
Step 2:
New cylinder power = (Power meridian which was not taken as the sphere in step 1) – (Power meridian which was taken as the sphere in step 1)
New cylinder power = +3.00 – (-2.00)
New cylinder power = +5.00 DC
Step 3:
New cylinder axis = 90 degrees (similar to meridian which was taken as the sphere pointing at or axis of the sphere which was not taken as the sphere in step 1).
It might sound a little bit confusing but remember power which is written on a particular axis represent the power meridian and 90 degrees apart from that will be the axis meridian of that power.
Final Sphero cylinder power = -2.00 DS / +5.00 DC X 90
For more information click video below:
Lecturer (Nethradhama School of Optometry)
Moptom

