A lensometer is an optical instrument that is used to determine the refractive power and the prescription of eyeglasses or contact lenses. It is a crucial tool in the field of optometry. Mainly used for measuring the back vertex power and front vertex power
Two types of lensometer are available
- Manual lensometer
- Automatic lensometer
Manual lensometer
The lensometer working is based on the principle of “Optometer”. Usually, the optical principle developed by “Badal” is preferred over other principles (non-Badal). Badal principle utilizes a plus lens in such a way so that its posterior focal plane coincides with the anterior focal plane of the eye which keeps image size contact while varying target distance and stimulus to accommodation. This optical system is telecentric in both the object and image space, that is the rays are parallel.
Optics of manual lensometer
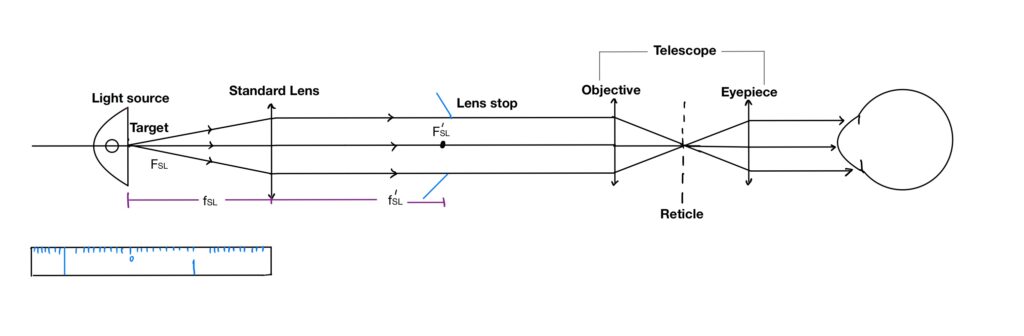
FSL is the primary focal point of the lens.
F/SL is the secondary focal point of the lens
A target (mires: the set of two perpendicular lines), is behind a standard lens (SL) of a known power (commonly +20.00 to +25.00). The target is placed at the anterior focal point of the standard lens so when converging rays come from the target and pass through the standard lens, these rays exit parallel. This is viewed through a telescope focused on an object which is at infinity and a clear image of mires is seen. In this optical system distance between the target and the standard lens can be altered.
So when an unknown power lens is a position between the standard lens and telescope which is also the secondary focal point of the standard lens. The whole optics of the lensometer disturb and the mire seen by the telescope will not be clear because the telescope only shows the mire clearly when rays enter parallel to it. The target is then moved back and forth until it is sharply focused as viewed through the eyepiece of the telescope.
At this point, the target object image position will be related to newton’s relationship’s
xx/ =fSL f/SL
Where fSL and f/SL are the primary and secondary focal lengths of the standard lens.
x is the distance from the primary focal point of the standard lens to the target.
x/ is the distance from the secondary focal point of the standard lens to the image of the target. The distance x/ will be the back vertex focal length of the unknown lens.
According to newton relationship
xx/ =fSL f/SL
xx/ =(1/FSL) (1/FSL)
Because fSL or f/SL= 1/FsL
x (1/F(unknown lens)) = (1/FSL) (1/FSL)
X/ = focal length of unknown lens
F(unknown lens) = x F2SL
where F(unknown lens) = power of unknown lens
FSL = Power of known lens
x = distance of target (mires) from the primary focal point of the standard lens
So if the unknown lens is of plus power, after focusing mires the target will be somewhere between the primary focal point of the standard lens and the standard lens. if the unknown lens is of minus power, after focusing mires the target will be somewhere outside the primary focal point of the standard lens when sharply focused.
Suppose we have to find the unknown power of the lens placed in the lens stop of the lensometer and the distance of mire from the primary focal point is +2 cm and the standard lens power is +20DS. Calculate unknown lens power.
F(unknown lens) = x F2SL
F(unknown lens) =0.02 X 20 2
F(unknown lens) = +8.00 DS
Remember if the target is outside the primary focal point of the standard lens x will be written in minus because we will measure the distance from right to left which is against sign convention.
Parts of manual lensometer:

The procedure of lensometer:
After calibration of the lensometer, place the unknown power lens in the lens stop
I. SINGLE VISION LENSES
a) FOR SPHERICAL LENS:
Rotate the Power Drum until the mires inside the lensometer get clear. Read the reading from Power drum which will give the actual power of eyeglasses.
b) FOR SPHEROCYLINDRICAL POWER
Step 1: Rotate the power drum until 1st meridian of the mire is clear and note down the power of 1st meridian from the power drum.
Step 2: Again, rotate the power drum until the 2nd meridian is clear but the 1st meridian gets blur note down the power of the 2nd meridian from the power drum and the axis from the reticule.
Step 3: Final power will be given by:
Spherical power = power of 1st meridian
Cylindrical power= power of 2nd meridian – power of 1st meridian
Axis = axis of 2nd meridian
II. FOR BIFOCAL LENS
Step 1: Measure the power of distance portion in the same way as single-vision glasses
Step 2: Measure the power of the near portion in the same way as single-vision glasses
Step 3: Near add will be given by the algebraic difference between the distance reading of the sphere power and the reading portion of sphere power.
Example 1:
Distance power +3.00DS
Near power +6.00DS Near add will be given by (near power – distance power)
= +6.00-(+3.00)
NEAR ADD =+3.00
Example 2:
Distance power -0.50DS
Near power +2.50 DS
Near add will be given by (near power – distance power)
= +2.50-(-0.50)
NEAR ADD =+3.00
Example 3:
Distance power -4.00DS/-1.00DC X 90
Near power -2.00DS/-1.00DC X 90
Near add will be given by (near power – distance power)
= -2.00DS-(-4.00)DS
NEAR ADD =+2.00DS
More more information check our link below
Lecturer (Nethradhama School of Optometry)
Moptom
