Compounding and resolving prism

Introduction

In a few cases of prism prescriptions, where both horizontal and vertical prisms are required to correct the deviation. In such a case, one single prism can be computed in the manufacturing process to have the exact same result as the combination of the two specified prisms.

Compounding prism

Compounding prism refers to the technique of combining two prisms in power and base orientation to create a single prism that has the same properties as both.

Resolving prism

The act of taking a prism with an oblique base orientation and expressing it as two prisms with perpendicular bases are known as compounding prisms opposite. A resolving prism is the process of splitting an oblique prism into two perpendicular halves.

Steps of compounding prism

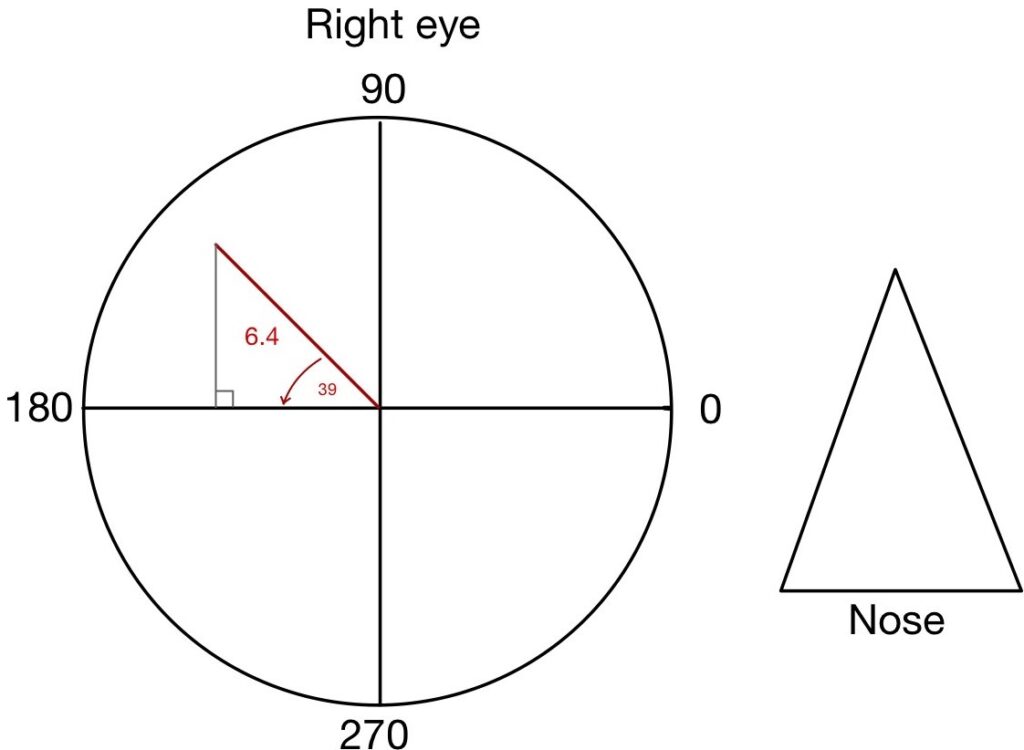
Example: Compound a prism 4 Δ Base up and 5 Δ Base out into a single resultant effect for the Right eye.

Step 1: Draw a Circle, divide the circle into 4 equal quadrants (vertically and horizontally), mention the nose direction and specify the axis of the Circle. Remember axis always runs anticlockwise and will be similar for both the right and left eye.

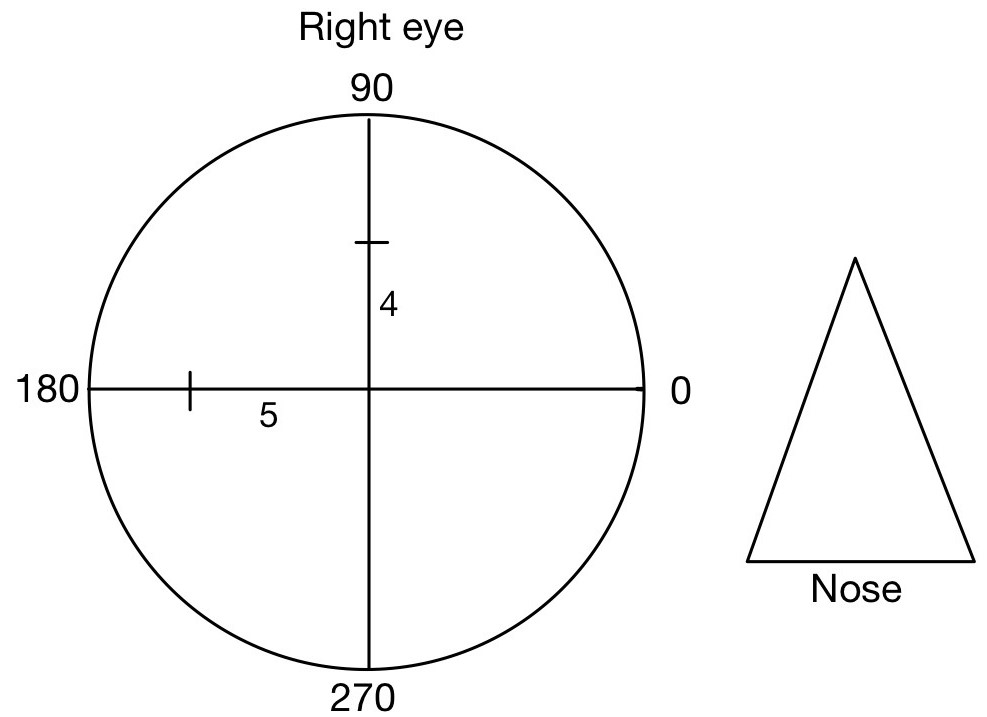
Step 2: Draw both horizontal and vertical prisms in scale and mention the length of the scale equal to the power of prims.

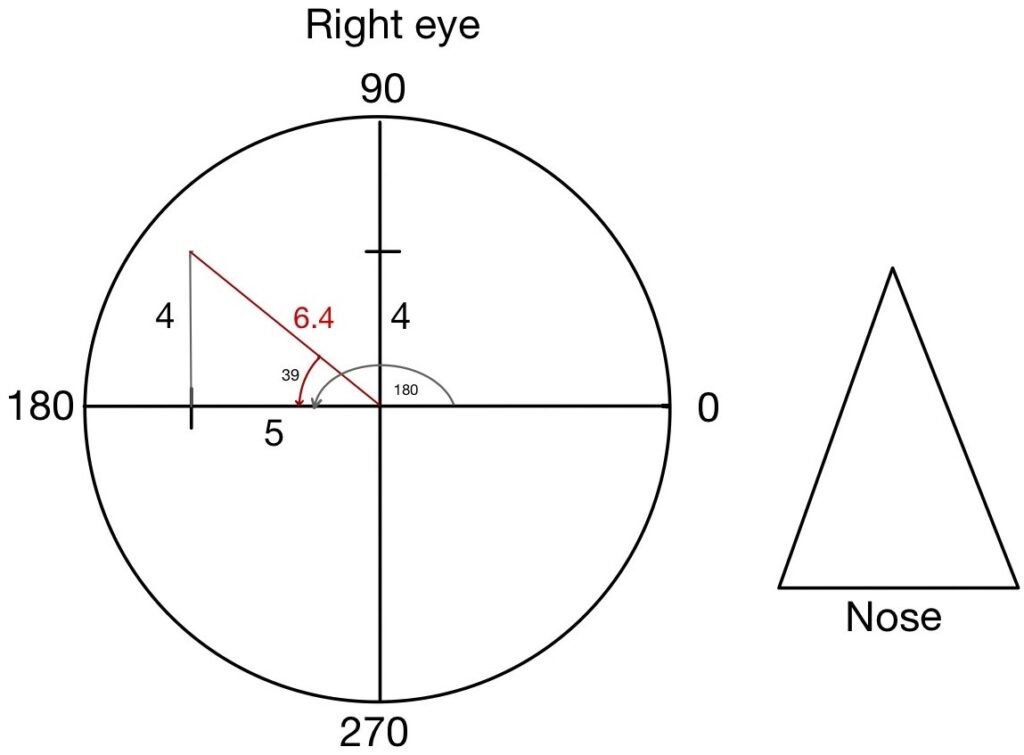
Step 3: Draw a right angle triangle with known horizontal and vertical sides (equal to the power of prism). The resultant prism (R) will be given by a vector that starts from the circle center and ends at the point representing the known horizontal and vertical sides

Step 4: To calculate the prism power of the resultant prism (R) apply Pythagoras theorem

R² = Adjacent² + Opposite²

R = √ (5² + 4²)

R = 6.4 Δ

Step 5: To find the angle of the triangle (Ø) use the Tan formula

Tan Ø = the ratio of the lengths of the opposite and adjacent sides

OR

Tan Ø = the ratio of the perpendicular and base side

Tan Ø = 4/5 = 0.8

Ø = Tan^-1 0.8

Ø = 38.66

Ø = 39 (approx.)

Step 6: As prism orientation is calculated from zero, so we need to find how far prism base orientation is from zero.

180 – 39

141

Step 7: Write down the prism prescription in 180 notation or 360 notation

6.40 Δ Base up out, Base 141 (180 Notation)

6.40 Δ Base 141 (360 Notation)

Click video below

Steps of Resolving a Prism

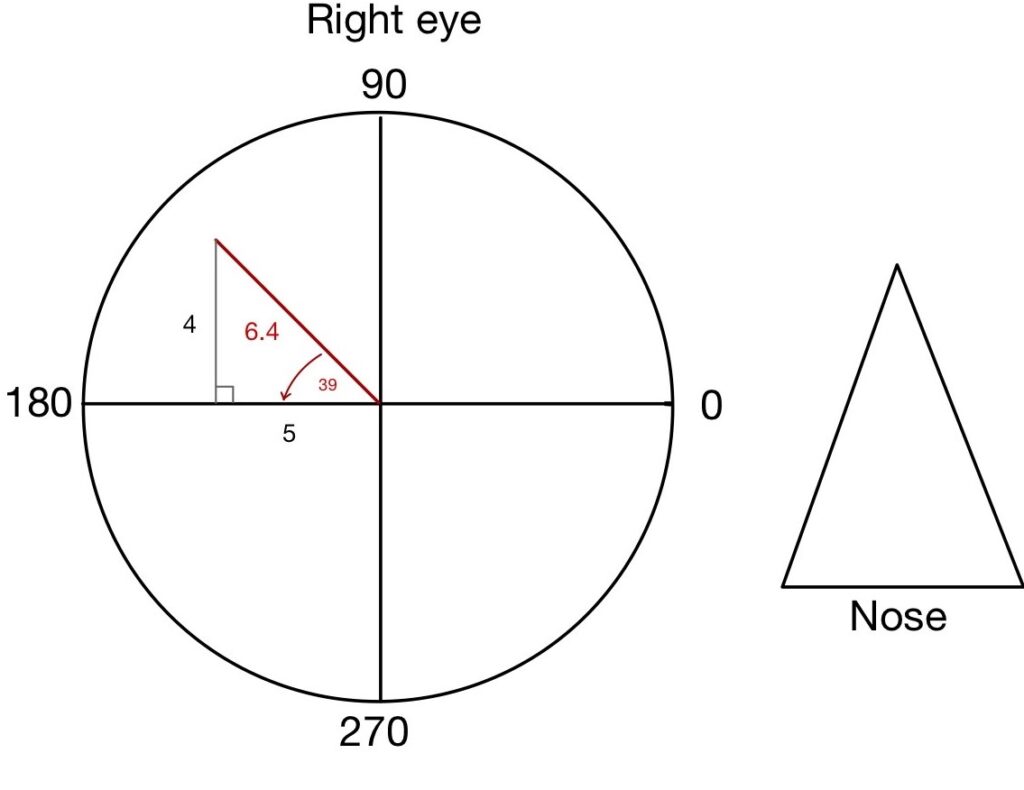
Example: 6.40 Δ Base 141

Step 1: Draw a Circle, divide the circle into 4 equal quadrants (vertically and horizontally), mention the nose direction and specify the axis of the Circle. Remember axis always runs anticlockwise and will be similar for both the right and left eye.

Step 2: Draw a prism in vector form, where the length of the vector will be equal to prism power and Base orientation will be drawn.

Step 3: Draw a right eye triangle and calculated the angle (Ø) of right eye triangle

Step 4: Adjacent and opposite sides of the triangle will be calculated using Cos and Sin formula

Sin Ø = the ratio of opposite side and hypotenuse

Or

Sin Ø = the ratio of the perpendicular side and hypotenuse

Cos Ø = the ratio of the adjacent side and hypotenuse

Or

Cos Ø = the ratio of the Base side and hypotenuse

Sin 39 = opposite side / 6.4

Opposite side = Sin 39 x 6.4  

Opposite side = Sin 39 x 6.4  

Opposite side = 4 Δ Base 90

Cos 39 = Adjacent side / 6.4

Adjacent side = Cos 39 x 6.4

Adjacent side = 5 Δ Base 180

Step 5: Write power in prescription form

Horizontal = 5 Δ Base out

Vertical = 4 Δ Base up

Click video below

To learn how to combine two oblique prisms to single resultant prism watch video below