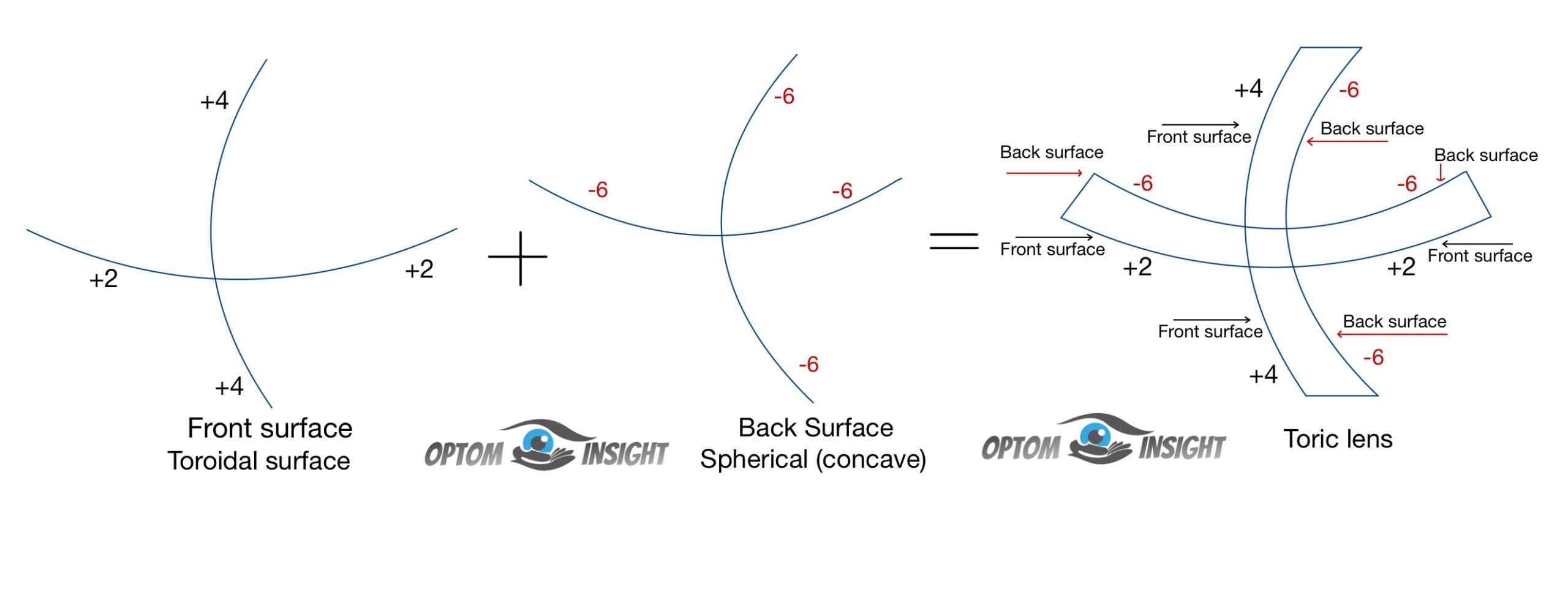
What is a Toric lens?
A toric lens is defined as a lens which has one surface toroidal (one of the principal meridians is more curved than the other principal meridian) and another surface of the lens is spherical (convex or concave).
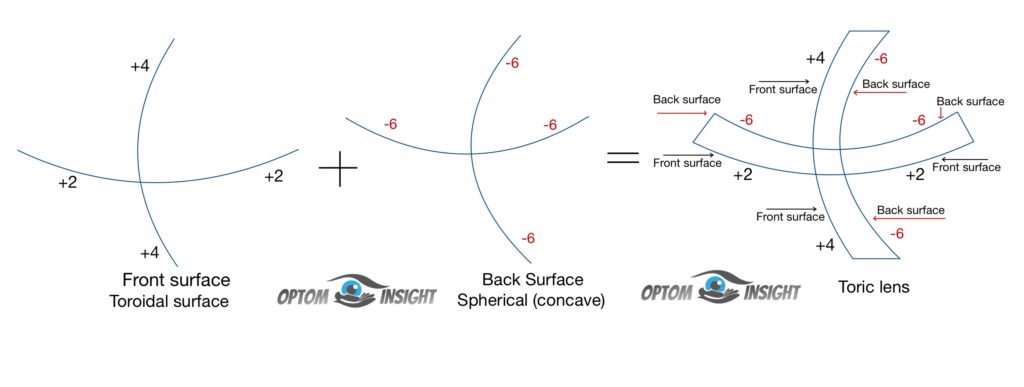
What is Toric transposition?
It is a method which enables, the Toric lens to be exactly defined in terms of surface power. Suppose we have power which equals +2.00 DS / +3.00 DC X 90, this way of writing the prescription does not tell us exactly, what is the surface power of the front and back surface of the lens. That is where Toric transposition plays an important role if one wants to know the exact surface power of the front and back surface of the lens or how much power is to ground on each surface so it matches above mention prescription.
- The base curve must be specified if the toric prescription is required.
- The principal meridian of the toroidal surface having weaker power is known as a “Base curve (BC)”
- The principal meridian of the toroidal surface having the highest power is known as a “Cross curve (CC)”
Steps of toric transposition
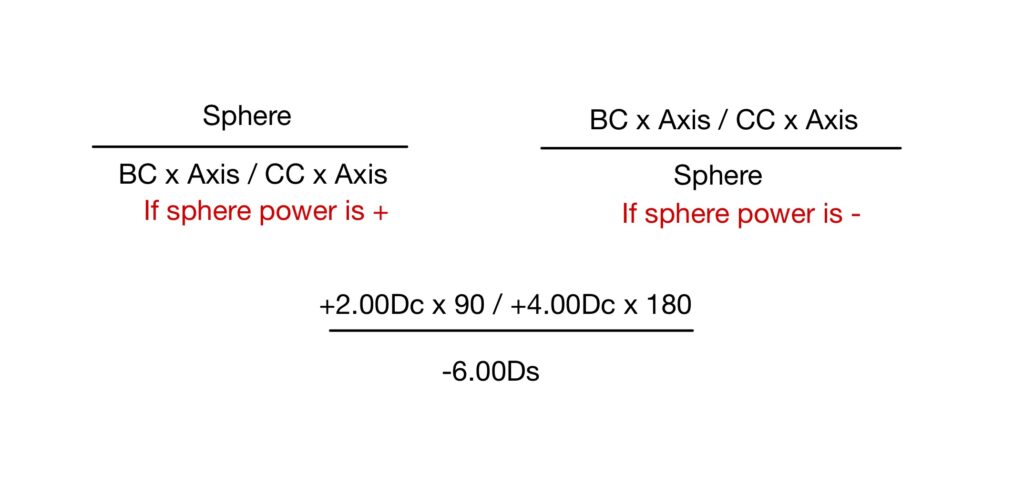
Example: -2.00 DS / -2.00 DC X 90 BC = +2.00
Step 1: The sign of the Base curve and cylinder (of sphero cylinder prescription) should be similar. If not transpose the sphero cylinder prescription to alternate sphero cylinder form, so that the base curve and cylinder are of the same sign.
-4.00DS / +2.00 DC X 180
Step 2: Calculate require the power of a spherical surface, this is obtained by subtracting the base curve from spherical power.
Require power of spherical surface = Sphere power of sphero cylinder prescription found in step 1 – Base curve.
Sph surface = Sph – BC
Sph surface = -4.00 – (+2.00) = -6.00 DS
Step 3: Write base curve power as it is and the axis will be perpendicular to the axis of the cylinder found in step number 1.
BC = +2.00 DC X 90
Step 4: To find the Cross curve, add the required cylinder to the base curve power with its axis similar to the cylinder of sphero cylinder power found in step 1.
CC = Require cylinder (equal to cylinder power of sphero cylinder prescription found in step 1) + Base curve.
CC = RC + BC
CC = +2 + (+2)
CC = +4.00 DC X 180
Step 5: Complete the toric formula which is given by
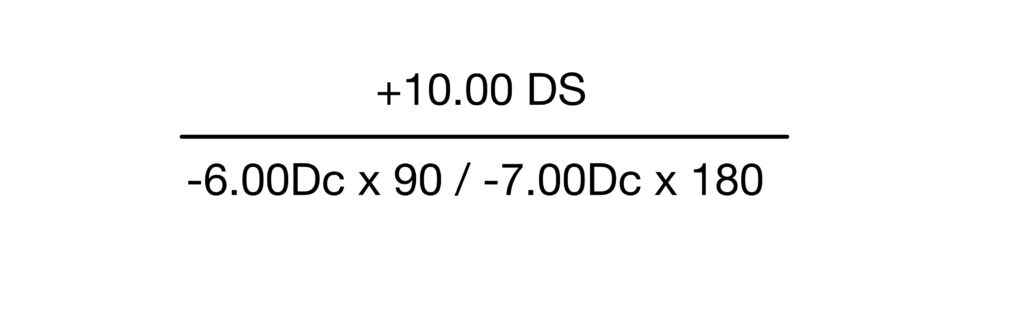
Example 2:
+4.00 DS / -1.00 DC x 180 BC = -6.00
Step 1: No need to transpose as cylinder and BC signs are similar.
Step 2: Sphere surface = Sph – BC
+4.00 – ( -6.00)
+10.00 DS
Step 3: BC = -6.00 DC X 90
Step 4: CC = RC + BC
-1.00 + (-6.00)
-7.00 DC X 180
Step 5
Click below link: to learn more about “Optometric optics”
https://optominsight.com/category/optometric-optics/
Lecturer (Nethradhama School of Optometry)
Moptom